Quaternion Weighted Average
31/12/2023
How do we find the weighted average of a set of quaternions?
This is not immediately obvious, in particular given that a quaternion and its negation represent the same rotation - so just doing a normal weighted sum of the raw 4d quaternion values is not going to work.
Well, here is a simple solution you might have seen used in various places:
quat quat_average_basic(
const slice1d<quat> rotations,
const slice1d<float> weights)
{
quat accum = quat(0.0f, 0.0f, 0.0f, 0.0f);
// Loop over rotations
for (int i = 0; i < rotations.size; i++)
{
// If more than 180 degrees away from current running average...
if (quat_dot(accum, rotations(i)) < 0.0f)
{
// Add opposite-hemisphere version of the quaternion
accum = accum - weights(i) * rotations(i);
}
else
{
// Add the quaternion
accum = accum + weights(i) * rotations(i);
}
}
// Normalize the final result
return quat_normalize(quat_abs(accum));
}
Essentially we just keep a running average and flip any quaternions that are on the opposite hemisphere to our running average. We then normalize the final result, and can take the version of this average rotation closest to the identity rotation using the quat_abs function if we like.
This is simple and works pretty well in most cases - in particular if the rotations in the set are already similar.
There are, however, a few problems we might encounter with this method: first - because we are using a running average the result of this function can actually change depending on the order of the provided quaternions.
For example, here is the rotation we get (shown on the right) if we apply this averaging function to sets of randomly generated quaternions (shown on the left) with a toggle to reverse the order in which we provide the quaternions to the function:
As you can see, sometimes the result is the same, but sometimes it can be really quite different. Not a desirable property of an averaging function!
Another issue with this method is that the result it produces has many unnecessary discontinuities, and can often suddenly jump to a new result as we change the rotations in the set. We can see this if we slowly adjust one of the rotations in the set:
For large sets of quaternions that are similar to each other this might not be an issue. But for smaller sets of quaternions or quaternions with large angular differences this can (like the nlerp function) make sudden jumps when the hemisphere of one of the quaternions changes. In fact, if we run this function on just two quaternions, the result is identical to nlerp.
So is there a better way to compute the average rotation? Yes - although first we need to think a bit more about what we actually want an average function to give us. One idea is this: we want the average rotation of a set of rotations to be a rotation which is as close as possible to all the rotations in that set. More specifically we can say that we want the average rotation of a set to be a rotation which has the smallest sum of squared distances to all the rotations in that set.
The derivation for how to compute this is a little complex (described in this paper), but the final implementation can be relatively simple. First we compute a weighted sum of the outer product of all our quaternions as a 4x4 matrix:
mat4 accum = mat4_zero();
// Loop over rotations
for (int i = 0; i < rotations.size; i++)
{
quat q = rotations(i);
// Compute the outer-product of the quaternion
// multiplied by the weight and add to the accumulator
accum = accum + weights(i) * mat4(
q.w*q.w, q.w*q.x, q.w*q.y, q.w*q.z,
q.x*q.w, q.x*q.x, q.x*q.y, q.x*q.z,
q.y*q.w, q.y*q.x, q.y*q.y, q.y*q.z,
q.z*q.w, q.z*q.x, q.z*q.y, q.z*q.z);
}
Once we have this, the average quaternion as given by the above definition, will be exactly equal to the largest eigenvector of this 4x4 matrix. This can be computed using the power iteration method (which you may remember from my previous article on Joint Limits):
vec4 mat4_svd_dominant_eigen(
const mat4 A,
const vec4 v0,
const int iterations,
const float eps)
{
// Initial Guess at Eigen Vector & Value
vec4 v = v0;
float ev = (mat4_mul_vec4(A, v) / v).x;
for (int i = 0; i < iterations; i++)
{
// Power Iteration
vec4 Av = mat4_mul_vec4(A, v);
// Next Guess at Eigen Vector & Value
vec4 v_new = normalize(Av);
float ev_new = (mat4_mul_vec4(A, v_new) / v_new).x;
// Break if converged
if (fabs(ev - ev_new) < eps)
{
break;
}
// Update best guess
v = v_new;
ev = ev_new;
}
return v;
}
This gives the following more accurate quaternion averaging function:
quat quat_average_accurate(
const slice1d<quat> rotations,
const slice1d<float> weights)
{
mat4 accum = mat4_zero();
// Loop over rotations
for (int i = 0; i < rotations.size; i++)
{
quat q = rotations(i);
// Compute the outer-product of the quaternion
// multiplied by the weight and add to the accumulator
accum = accum + weights(i) * mat4(
q.w*q.w, q.w*q.x, q.w*q.y, q.w*q.z,
q.x*q.w, q.x*q.x, q.x*q.y, q.x*q.z,
q.y*q.w, q.y*q.x, q.y*q.y, q.y*q.z,
q.z*q.w, q.z*q.x, q.z*q.y, q.z*q.z);
}
// Initial guess at eigen vector is identity quaternion
vec4 guess = vec4(1, 0, 0, 0);
// Compute first eigen vector
vec4 u = mat4_svd_dominant_eigen(accum, guess, 64, 1e-8f);
vec4 v = normalize(mat4_mul_vec4(accum, u));
// Average quaternion is first eigen vector
return quat_abs(quat(v.x, v.y, v.z, v.w));
}
(Note: quat here stores components in wxyz order while vec4 stores components in xyzw order...)
The distance this algorithm minimizes is effectively the squared distance between rotation matrices. i.e. it minimizes the sum of the squared distances between the rotation matrix of this average quaternion, and the rotation matrices of every quaternion in the set. And since we are talking in terms of distances between matrices, specifically it minimizes the sum of the squared Frobenius distances.
For rotations, the Frobenius distance between the rotation matrices is actually equivalent to the sin of half the angle between the two rotations:
float quat_frobenius_distance(quat q, quat p)
{
// Compute the difference between two quaternions
quat d = quat_abs(quat_mul_inv(q, p));
// Compute the half-angle of that difference
float halfangle = acosf(clampf(d.w, -1.0f, 1.0f));
// Compute the sin of the half angle
return sinf(halfangle);
}
This squared sin of the half-angle may seem like an odd kind of distance to be minimizing. It might seem more intuitive to try to minimize the sum of the squared angular differences directly, however the square of the sin of the half angle has some nice properties - it is similar to the square of the half-angle itself for small angles, but it plateaus smoothly around an angular difference of pi radians (i.e. when the two rotations are at their most different), which gives us smooth continuous behavior for the averaging function:
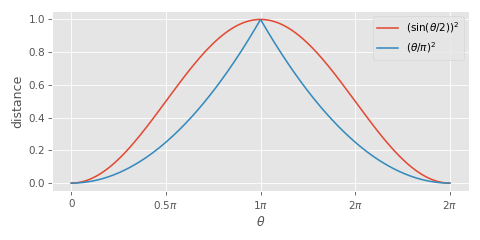
Although more expensive to compute (and the constant time overhead is quite large if you have just a few rotations in the set), this accurate algorithm for averaging quaternions solves our issues with the previous method. It's independent of the order we provide the rotations:
And it does not jump when we slowly adjust the rotations:
To test that this algorithm does what it states, we can compute the sum of the squared sin-half-angles between our average rotation and the rotations in the set. This will help us verify that this algorithm really does produce a smaller result than our basic method:
So yes, this method really does produce an average rotation with a smaller sum of squared sin-half-angles than our first basic method.
If you want to play around with the demo shown in this article the source code can be found here.
And that's about it. If you want to read more, there are lots of other resources online covering the same topic from which most of this article is taken! And as usual, thanks for reading.
Appendix: Weighted Average of Relative Rotations
As I discussed in my article on Joint Limits, it's really important when dealing with quaternions to keep in mind if they represent relative rotations or absolute rotations - i.e. are these rotations of something relative to something else meaningful, or are they just orientations in the world space that are not relative to anything in particular.
And as also discussed in that article - if we have joint rotations representing a character's pose, what these rotations are relative to is the pose we get when we set all rotations to the identity: the identity pose - something that is usually not at all a meaningful pose (which makes these rotations more like absolute rotations):
Just as how applying joint limits with respect to the identity pose does not work - just taking the raw average of quaternions with respect to the identity pose does not work either - and is what will produce the discontinuities and bad results we saw before.
void bone_rotations_weighted_average_raw(
slice1d<quat> blended_rotations,
const slice2d<quat> sample_rotations,
const slice1d<float> sample_weights)
{
assert(sample_rotations.rows == sample_weights.size);
assert(sample_rotations.cols == blended_rotations.size);
blended_rotations.zero();
for (int i = 0; i < sample_rotations.rows; i++)
{
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = blended_rotations(j) +
sample_weights(i) * quat_abs(sample_rotations(i, j));
}
}
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = quat_normalize(blended_rotations(j));
}
}
For example, this is the result we get if we take the raw weighted average of the quaternion values of these three different poses, as compared to the "accurate" method I presented above:
Similarly, we could do the weighted average in the log space instead...
void bone_rotations_weighted_average_log(
slice1d<quat> blended_rotations,
slice1d<vec3> accum_rotations,
const slice2d<quat> sample_rotations,
const slice1d<float> sample_weights)
{
assert(sample_rotations.rows == sample_weights.size);
assert(sample_rotations.cols == blended_rotations.size);
assert(sample_rotations.cols == accum_rotations.size);
accum_rotations.zero();
for (int i = 0; i < sample_rotations.rows; i++)
{
for (int j = 0; j < sample_rotations.cols; j++)
{
accum_rotations(j) += sample_weights(i) *
quat_log(quat_abs(sample_rotations(i, j)));
}
}
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = quat_exp(accum_rotations(j));
}
}
but this is not any better...
The problem is that these rotations are being averaged "around" this identity pose - a pose which is not meaningful to take an average around - and just moving to the log space does not change this.
If we instead transform all our rotations to be relative to some meaningful character pose such as the skinned rest pose...
...then taking the weighted average makes a lot more sense and gives a lot better results.
void bone_rotations_weighted_average_raw_ref(
slice1d<quat> blended_rotations,
const slice1d<quat> reference_rotations,
const slice2d<quat> sample_rotations,
const slice1d<float> sample_weights)
{
assert(sample_rotations.rows == sample_weights.size);
assert(sample_rotations.cols == blended_rotations.size);
assert(sample_rotations.cols == reference_rotations.size);
blended_rotations.zero();
for (int i = 0; i < sample_rotations.rows; i++)
{
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = blended_rotations(j) + sample_weights(i) *
quat_abs(quat_inv_mul(
reference_rotations(j), sample_rotations(i, j)));
}
}
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = quat_abs(quat_mul(
reference_rotations(j), quat_normalize(blended_rotations(j))));
}
}
Here is what happens visually if we make these rotations relative to the "reference pose" before taking the average:
Now we can see that the result is really similar to our "accurate" method from before.
This method is faster to compute since we don't need to compute an eigenvector which is very nice. Also, in some cases it might even give more desirable results since it will effectively average a rotation of -170 degrees away from the reference pose in one direction, and 170 degrees away from the reference pose in the opposite direction back to the reference pose itself. Our "accurate" method on the other hand would average these two rotations to a full rotation of 180 degrees. Which behavior you prefer here obviously depends on the application.
Notice that the result of our "accurate" method is unchanged by using rotations relative to the reference pose or not - it always treats rotations as absolute rotations, exactly as hoped for!
Due to the way the quaternion space is shaped, the weighted average in the raw quaternion space will tend to reduce the impact of large rotations close to 180 degrees. If we want to take these into account more fairly it is better to do the averaging in the log space.
void bone_rotations_weighted_average_log_ref(
slice1d<quat> blended_rotations,
slice1d<vec3> accum_rotations,
const slice1d<quat> reference_rotations,
const slice2d<quat> sample_rotations,
const slice1d<float> sample_weights)
{
assert(sample_rotations.rows == sample_weights.size);
assert(sample_rotations.cols == blended_rotations.size);
assert(sample_rotations.cols == accum_rotations.size);
assert(sample_rotations.cols == reference_rotations.size);
accum_rotations.zero();
for (int i = 0; i < sample_rotations.rows; i++)
{
for (int j = 0; j < sample_rotations.cols; j++)
{
accum_rotations(j) += sample_weights(i) *
quat_log(quat_abs(quat_inv_mul(
reference_rotations(j), sample_rotations(i, j))));
}
}
for (int j = 0; j < sample_rotations.cols; j++)
{
blended_rotations(j) = quat_abs(quat_mul(
reference_rotations(j), quat_exp(accum_rotations(j))));
}
}
However, the difference is fairly small in this example - and the computational cost is slightly larger:
If you're interested in learning more about making rotations relative to a reference pose, check out this old video by Casey Muratori.
To summarize:
If you have a "reference" you want to average around then transform your rotations relative to that reference and either average the raw quaternion values, or average in the log space (if you want slightly better quality at the cost of some performance loss).
If you have no "reference" or are averaging quaternions that are not relative to anything meaningful, use the "accurate" quaternion averaging function as presented above.
In fact, if you have no "reference" but know the quaternions in your set are going to be similar to some other set, one approach I've seen before is to use the "accurate" method ahead of time on this other set to extract a reference which future rotations can be more performantly averaged around later on. So that's an option too!